推荐系统已广泛应用在诸多领域中。在社交网络中，可推荐志趣相投的朋友；在金融市场，可推荐适合自己的股票基金等理财产品；在婚恋市场中，可推荐适合自己的另一半。通过推荐系统，还可根据自己的喜好推荐个性化的新闻、视频、音乐、图书、游戏、食品、衣物等。因此，推荐系统具有极大的潜在价值。亚马逊就是通过引入推荐系统后，极大提高了用户活跃度及市场销售额。

类型

• 手工生成的推荐系统
  • 早期的门户网站，其内容都是手工编辑选择的
• 聚合推荐系统
  • KTV中歌曲点播排行榜/电影票房排行榜/最新上架商品等
• 千人千面的推荐系统(重点介绍)
  • Amazon商品推荐/Netflix电影推荐/今日头条新闻推荐 (以用户为中心进行推荐)

数学模型

令$U$表示用户集合，$P$表示物品集合。则可用两个集合的笛卡尔积(两个集合元素组成的所有可能的有序对集合)表示推荐系统的输出，即$U\times P\longmapsto R$。其中$R$表示用户对物品的喜好程度。具体地，以电影为例

用户集合：

物品集合：

推荐值矩阵(空缺值表示用户没看电影或看了但没有进行打分)：

关键问题

• 收集数据，建立推荐值矩阵
  • 数据具有时效性。一个用户的喜好会随时间的变化而变化
• 从推荐值矩阵的已知数据预测未知的数据
  • 推荐系统的核心功能
• 建立评价体系，检验推荐效果，是否做到了有效推荐

收集数据

• 显式收集
  • 请用户为物品打分、点赞和评价
  • 若用户很少打分、评论的话，则收集的数据就会不完整
• 隐式收集(通过用户行为来推断用户对物品的喜好程度)
  • 视频网站：用户行为特征有快进、重播等
  • 购物网站：用户行为特征有购买、退货等

从推荐值矩阵的已知数据预测未知数据

关键挑战

• 当用户和物品数量都比较大时，推荐值矩阵通常是一个非常大的稀疏矩阵，矩阵中有大量缺失值。即大多数用户对大多数商品没有喜好程度的表现。
• 冷启动问题。即新出现的物品还没有任何用户为它打分以及新用户没有任何的打分行为

矩阵分解(常用方法)

• 基本思想：将推荐值矩阵$R$分解为矩阵$U$和$P$,使得$U$和$P$的乘积得到的矩阵$R^*$中的元素值与$R$中的已知元素的值非常接近，则$R^*$中的对应于$R$中的未知的元素值就是预测值。具体地，如下图所示

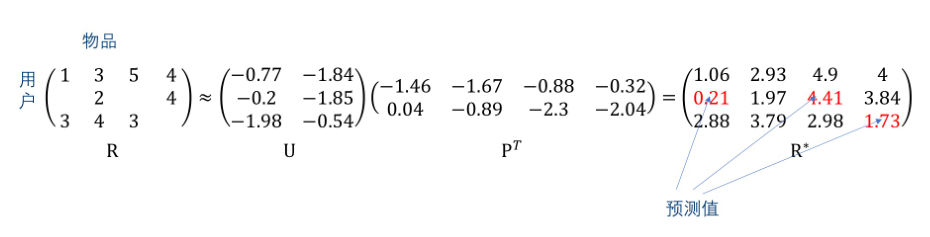
• 物理含义：$U$的每一行表示一个用户的画像向量，$P$的每一行表示一个物品的画像向量(上图中与$U$相乘的矩阵是$P^T$),而$U、P$的列数$k$是矩阵分解模型待确定的超参数，表示有多少个隐含因素决定了某个用户对某个物品的喜好程度，一般通过交叉验证来确定这个超参数。令$k=2$,上述矩阵分解的具体含义如下：
  • 推荐值矩阵中的元素值已知

  

  • 推荐值矩阵中的元素值未知

  

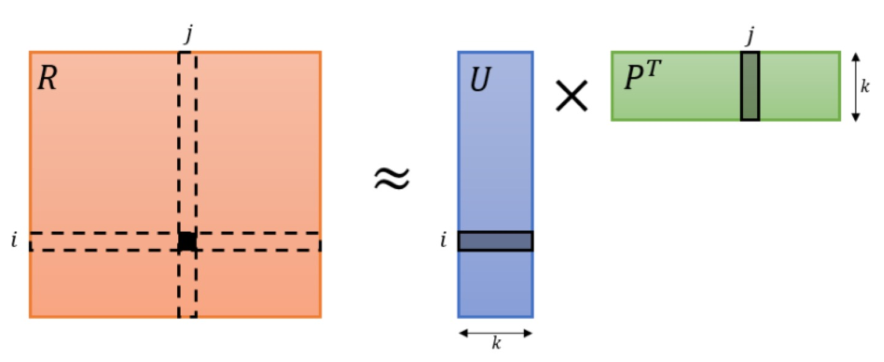
• 模型假设：评分($Rating$)矩阵$R\in \mathbb{R}^{m\times n}$包含了$m$个用户对$n$个物品的评分。假设评分矩阵可分解为用户矩阵$U\in \mathbb{R}^{m\times k}$和物品矩阵$P\in \mathbb{R}^{n\times k}$，使得$R\approx U\times P^T$。具体如下图所示。其中$k$是矩阵分解的秩，决定了$U,P$的维度。$R_{ij}$为评分矩阵第$i$行第$j$列的元素，且$R_{ij}\approx U_i\cdot P_j$。

• 模型目标函数：
  • 无正则化的：$\underset{U,P}{argmin}\sum_{\left( i,j \right) \in Z}{\frac{1}{2}\left( R_{ij}-U_i\cdot P_j \right) ^2}$
  • 有正则化的：$\underset{U,P}{argmin}\sum_{\left( i,j \right) \in Z}{\frac{1}{2}\left( R_{ij}-U_i\cdot P_j \right) ^2+\lambda \left[ \sum_{i=1}^m{\lVert U_i \rVert ^2}+\sum_{\boldsymbol{j}=1}^{\boldsymbol{n}}{\lVert P_i \rVert ^2} \right]}$

  其中$Z=\left\{ \left( i,j \right) \left\| R_{ij}\text{已知} \right. \right\}$

  • 基于上述目标损失函数，可通过梯度下降法求出未知矩阵参数$U,P$

• 优缺点

  优点

  • 相对于协同过滤 ，矩阵分解后预测一个值的计算量比较小。预测的计算就是求两个向量的点积，预测时的计算复杂度和用户以及物品数量无关
  • 相对于基于内容的推荐系统，矩阵分解很好的利用了其他用户对物品打分的数据

  缺点

  • 类似于协同过滤，矩阵分解也具有冷启动的问题，对于一个新用户或新物品，因没有相关的喜好数据，无法做出推荐。
  • 假设了推荐值可通过用户画像向量和物品画像向量的点积得到，相当于默认了线性关系，事实上可能是更加复杂的非线性关系

推荐系统的评估

• 离线评估
  • 将数据三七分，形成测试数据集合$T$和训练数据集合$U$，利用$U$来训练一个推荐系统，然后在$T$上做出预测，比较预测和真实的平均绝对误差来进行评估

• 问卷调查

• 在线测试(A/B测试)
  • 同一批用户分成两组分别在老系统与新系统进行推荐，比较两组用户的推荐效果

总结

• 世界上没有一种算法在解决任何问题的情况下都优于另一种算法
• 组合多种不同的算法，可以有效提升整体的性能

实战

短视频推荐

• 源文件 Short.Video.Recommender.ipynb

• 数据集 u.data

图书推荐

• 源文件 Book.Recommender.ipynb

• 数据集 book_ratings.dat