概述
K-means是一种聚类(模型)算法,属于非监督学习。对于给定的样本集,按照样本之间的距离大小,将样本集划分成$K$(事先确定的超参数)个互不相交的子集,每个子集称为一个簇(cluster),簇中的每个样本有着相似的特征,这个相似特征以簇的中心点表示。K-means常用于用户分群、行为聚类、图像分割等情形。
假设
- 该算法假设聚类结构能通过一组原型刻画。其中原型是指样本空间中具有代表性的点。(K-means属于原型聚类中的一种,具体见周志华的西瓜书)
数学描述
给定样本集,$x_i$表示$d$维向量,K-means聚类后的$K$个簇为。其目标函数为
其中 表示各个簇中每个样本点到该簇中心点的(欧式)距离之和,表示簇的均值(中心点),与为模型待学习参数。互不相交,且$C_1+C_2+\cdots+C_K=D。$
K-means采用贪心策略,通过迭代来求解上述目标函数(最小化距离和)。具体步骤为
$step1$: 随机初始化$K$个中心点,每个点代表每个簇的初始中心点。
$step2$: 对每个样本点$x_i$,将其分配到距离最近的中心点所在的簇(中心点已知,样本点所在的簇未知,相当于EM中的E步)以使目标函数最小,遍历完所有点后,得到初步的$K$个簇
$step3$: 对每个簇$k$,重新计算该簇的中心(样本点所在的簇,簇的样本点未知,相当于EM中的M步)以使目标函数最小,最终得到更新后的$K$个中心点
$step4$: 依此重复$step2$和$step3$,($step2$和$step3$表示一次迭代,和EM算法相似)直到聚类结果(中心点)保持不变,停止迭代。
下面给出K-means的迭代示意图,其中$K=2$
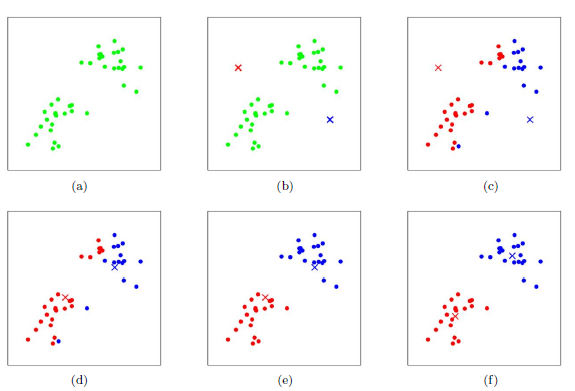
首先,给定二维空间上的一些样本点(图$(a)$),直观上这些点可以被分成两类;接下来,初始化两个中心点(图$(b)$的红色和蓝色叉子代表中心点),并根据中心点的位置计算每个样本所属的簇(图$(c)$用不同颜色表示);然后根据每个簇中的所有点的平均值计算新的中心点位置(图$(d)$);图$(e)$和$(f)$展示了新一轮的迭代结果;在经过两轮的迭代之后,中心点基本收敛。
几个问题
初始化问题
$K$个初始化中心点位置的选择对最终的聚类结果和运行时间都有很大的影响(因为目标函数为非凸函数,神经网络/HMM/CRF/LDA/GMM的目标函数也是一种非凸函数),因此需要选择合适的$K$个中心点。如果仅仅是完全随机的选择,有可能导致算法收敛很慢。K-Means++算法就是对K-Means随机初始化中心点方法的优化,其使选择的点之间的距离尽可能的大。
收敛性问题
K-means是EM算法的一个特例,而EM算法可以保证每次迭代,使得目标函数越来越小。即总是朝着收敛(convergence)的方向进行的。因此K-means通过不断迭代,一定可以收敛到目标函数的边界。
超参数$K$的确定
绘制不同$K$(横坐标)对应的损失函数(纵坐标)的曲线,其中由下降速率较快到较慢的转折点就是比较好的超参数$K$。
其他聚类模型
- GMM(原型聚类)
- DBSCAN(密度聚类)
- AGNES(层次聚类)
- Kernel K-means
优缺点
优点:
- 原理简单,实现容易,收敛速度快
- 聚类效果较优
- 算法的可解释度比较强,且在计算每个点到中心点的距离时可以并行计算
- 主要需要调参的参数仅仅是簇数$K$
缺点:
- $K$值的选取不好把握
- 若数据不平衡,则聚类效果不佳
- 采用迭代方法,得到的结果只是局部最优
- 对噪音和异常点比较的敏感