HMM
HMM是关于时序的概率有向图模型,属于生成模型。即先求解联合概率,再利用贝叶斯定理求条件概率。其描述了由一个隐藏的马尔科夫链生成不可观测的状态序列,再由各个状态生成一个观测序列的过程。
补充:概率有向图的联合概率
其中表示节点的(最近的)父节点。
HMM常用于序列标注(分词/POS/NER/SRL/语音识别/…)任务。即给定观测的序列,预测其对应的标记(状态序列)。可以假设待标注的数据是由隐马尔科夫模型(HMM)生成的,那么我们可通过HMM的学习(确定模型参数)与预测(确定最优隐状态序列)算法进行标注。
数学描述
HMM由初始状态概率分布向量、状态转移概率分布矩阵以及观测概率分布矩阵确定。
下面具体描述HMM的三个组成部分。
设是所有可能的状态集合,是所有可能的观测值集合,是可能的状态数,是可能的观测数。是长度为的状态序列,是对应的观测序列。
则
其中表示初始时刻处于某个状态的概率。
其中表示在时刻处于状态的条件下,下一时刻转移到状态的概率。
其中表示在时刻处于状态的条件下,观测到的概率。
初始状态概率向量和状态转移概率矩阵确定了隐藏的马尔科夫链,生成不可观测的状态序列。观测概率矩阵确定了如何从状态序列生成观测序列。 综上,HMM可由三元符号表示成。
HMM具体的数值例子(例10.1 盒子和球模型)见李航的《统计学习方法》
相关假设
由上述定义可知,HMM有如下假设
- 齐次马尔科夫性假设。即假设隐藏的马尔科夫链在任意时刻的状态只依赖于其前一时刻的状态,与其他时刻的状态及观测无关,也与时刻无关。
- 观测独立性假设。即假设任意时刻的观测只依赖于该时刻的马尔科夫链的状态,与其他观测及状态无关。
观测序列的生成
输入: 隐马尔可夫模型,观测序列长度
输出: 观测序列
- (1) 由初始状态概率分布,确定初始状态
- (2) 令
- (3) 由当前状态的观测概率分布阵,确定观测值
- (4) 由状态转移概率阵,确定下一时刻的状态
- (5) 令,如果,跳到(3);否则终止。
HMM在分词中的应用
假设有文本(观测)序列,HMM分词的任务就是根据序列进行推断,得到标记(状态)序列。即计算如下概率,使其值最大:
由贝叶斯公式可得
又序列是确定的,则为常值。所以只需使下式值最大
而右式中的、和分别是初始状态概率向量、状态转移概率矩阵和观测概率矩阵中的元素。当确定后,可通过维特比算法求出一个文本序列对应概率最大的分词标记序列,最终完成分词任务。
参数的确定
假设所给语料的格式如下:
- 文本序列(字典中共有N个字)
- 预测序列(Begin/Middle/End/Single/Other),分词任务中通常用BMES标记,此时隐状态个数为4
语料中的一个样本
- 请问今天南京的天气怎么样
- BEBEBESBEBME
1) 初始状态概率向量 统计每个句子开头的序列标记分别为的个数,然后除以总句子的个数,即得到了初始概率向量。
2) 状态转移概率矩阵 统计语料中前后序列标记间转移的个数。如统计语料中,在时刻标记为的条件下,时刻标记为出现的次数,类似的统计可得到4*4的矩阵,再将矩阵的每个元素除以相应行对应标记的总个数,保证行的概率和为1。最终得到状态转移概率矩阵。
3) 观测概率矩阵 统计语料中在某个标记下,某个观测值出现的个数。如统计语料中,在时刻标记为的条件下,时刻观测到字为”南“的次数。类似的统计得到一个4*N的矩阵,再将矩阵的每个元素除以语料中某个标记的总次数,保证行的概率和为1。最终得到观测概率矩阵。
维特比算法
由上面三组概率,确定一条概率最大的标记序列。即确定的标记序列使得式的值最大。
基于上述HMM的数学描述,先给出一般的维特比算法流程。
变量的定义
定义在给定模型参数条件下,时刻状态为时,所有可能的标注序列中,概率最大值记为
则
又当时刻标注序列状态确定时,则时刻的观测概率也是确定的(观测序列已知)。 因此由式的联合概率公式,可进一步写成
定义在时刻状态为时,所有可能的标注序列中,概率最大值时对应的时刻(前一时刻)的标注序列为
基于上述两个变量的定义,维特比算法的流程如下:
输入: 模型和观测序列
输出: 最优标注(状态)序列
(1) 初始化:
(2) 递推
,其中
(3) 终止(确定最后时刻所有可能的标注序列中概率最大时最后一个位置的标记)
(4) 回溯 (从后往前确定一个最优标注序列)
通过上述一去一回的迭代,最终可得最优标注序列。具体数值例子(例10.3)见李航的《统计学习方法》
基于上述描述,具体看一个简单的分词实战。假设给定文本:我爱中国。序列标注有四种状态。在确定标注序列时,每个字有4种可能的标注状态。如图所示
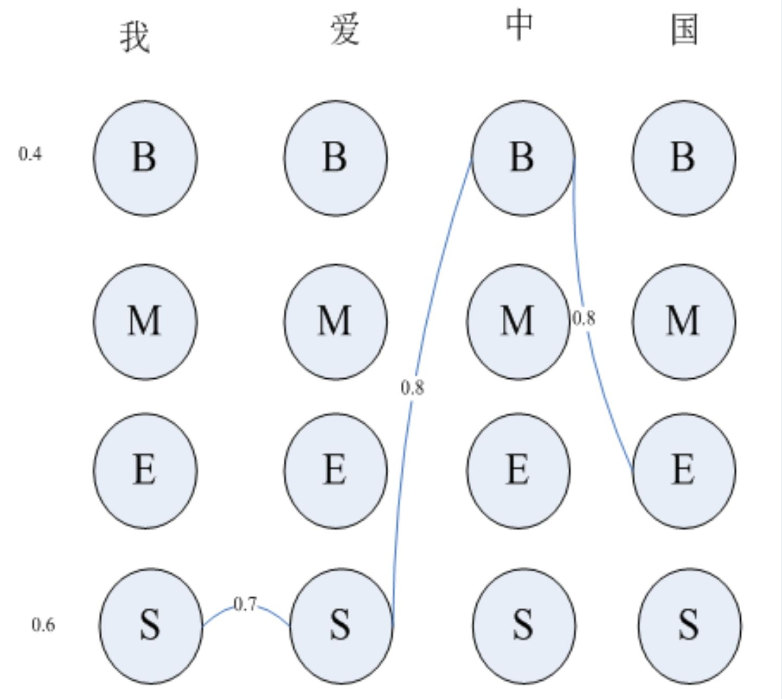
(1)初始化
(2) 递推
(3)终止,确定最后一个位置的标记
(4)回溯,确定最终的标注序列
最终可得序列
CRF
CRF结合了最大熵模型和隐马尔可夫模型的特点,是一种概率无向图模型(由无向图表示的联合概率分布,也叫马尔可夫随机场),属于判别模型。即直接求解条件概率。在NLP中,最常用的是线性链条件随机场。
与HMM相比,CRF具有更强的建模能力。其考虑了某一时刻的状态的上下文关系(上一时刻与下一时刻的状态)
概率无向图的因子分解
给定概率无向图模型,为上的最大团,表示中的节点集合(随机变量)。那么概率无向图(联合概率)可写成所有最大团上的势函数的连乘积形式,即
其中表示归一化因子,表示多种可能分布的集合,
条件随机场
设表示随机变量,若构成一个由图表示的概率无向图(马尔科夫随机场),即
对任意节点都成立,其中表示在图中与节点有边连接的所有节点,表示节点以外的所有节点,表示节点对应的随机变量。则称条件概率分布为条件随机场。
上述定义中并没有要求具有相同的结构。实际中常假设具有相同的图结构,常用的线性链结构如下图所示
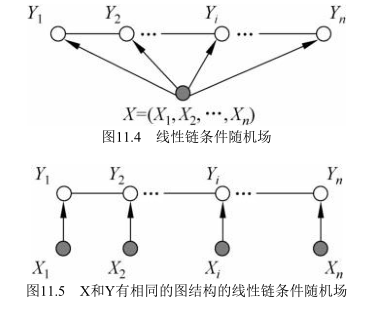
此时
最大团是相邻两个结点的集合。
线性链条件随机场定义如下: 设均为线性链表示的随机变量序列,在给定随机变量序列的条件下,若条件概率构成条件随机场,即满足如下性质
则称为线性链条件随机场。在标注问题中,表示观测序列,表示对应的标记序列(状态序列)。
(线性链)条件随机场的参数化形式
设为线性链条件随机场,则在随机变量取值为的条件下,随机变量取值为的条件概率具有如下形式:
其中
为归一化因子,求和是针对所有可能的标注序列进行的。
参数解释:
是定义在边上的特征函数,称为转移特征,依赖当前和前一个位置,是定义在节点上的特征函数,称为状态特征,依赖当前位置。分别为的权值,为模型待学习的参数。 通常,特征函数取值为1或0。
更进一步地,表示由给定序列预测的标注序列中相邻标注间的状态转移的得分, 表示某个观测序列被标注为序列的得分。
条件随机场由共同确定。
(tensorflow中的)条件随机场在NER中的应用
以序列标注任务中的命名实体识别()为例,详解tensorflow中的条件随机场。
假设命名实体识别任务的网络结构如图所示:
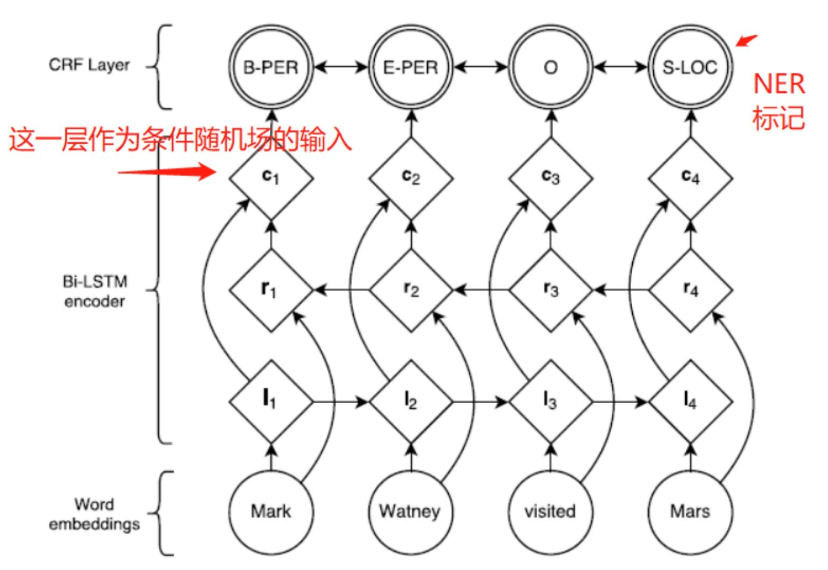
在上图中我们只关注与CRF相关的部分。CRF的输入(观测序列)为一个句子经过双向LSTM后的输出特征,输出(状态序列)为每个词对应的标记。训练阶段,利用真实的对,构造损失函数,通过极小化损失学习出CRF模型中的参数。预测阶段,直接将待标记的句子输入到网络中,利用维特比算法选取概率最大的序列作为最终的标记序列。
先看下tensorflow中对CRF损失函数的定义,其用于训练过程的参数估计
tf.contrib.crf.crf_log_likelihood(
inputs,
tag_indices,
sequence_lengths,
transition_params=None
)
其中inputs表示双向LSTM的输出,其形状为[batch_size, max_seq_len, num_tags],tag_indices表示输入句子中每个词对应的真实标签索引号,其形状为[batch_size, max_seq_len],sequence_lengths表示输入句子的真实长度,其形状为[batch_size],transition_params表示转移矩阵,其为待学习确定的CRF层的参数,其形状为[num_tags,num_tags]
接着看下其具体实现
def crf_log_likelihood(inputs,
tag_indices,
sequence_lengths,
transition_params=None):
"""Computes the log-likelihood of tag sequences in a CRF.
Args:
inputs: A [batch_size, max_seq_len, num_tags] tensor of unary potentials
to use as input to the CRF layer.
tag_indices: A [batch_size, max_seq_len] matrix of tag indices for which we
compute the log-likelihood.
sequence_lengths: A [batch_size] vector of true sequence lengths.
transition_params: A [num_tags, num_tags] transition matrix, if available.
Returns:
log_likelihood: A [batch_size] `Tensor` containing the log-likelihood of
each example, given the sequence of tag indices.
transition_params: A [num_tags, num_tags] transition matrix. This is either
provided by the caller or created in this function.
"""
# Get shape information.
num_tags = tensor_shape.dimension_value(inputs.shape[2])
# Get the transition matrix if not provided.
if transition_params is None:
transition_params = vs.get_variable("transitions", [num_tags, num_tags])
sequence_scores = crf_sequence_score(inputs, tag_indices, sequence_lengths,
transition_params)
log_norm = crf_log_norm(inputs, sequence_lengths, transition_params)
# Normalize the scores to get the log-likelihood per example.
log_likelihood = sequence_scores - log_norm
return log_likelihood, transition_params
crf_log_likelihood函数中先调用crf_sequence_score函数获取序列没有归一化的得分,具体实现如下:
def crf_sequence_score(inputs, tag_indices, sequence_lengths,
transition_params):
"""Computes the unnormalized score for a tag sequence.
Args:
inputs: A [batch_size, max_seq_len, num_tags] tensor of unary potentials
to use as input to the CRF layer.
tag_indices: A [batch_size, max_seq_len] matrix of tag indices for which we
compute the unnormalized score.
sequence_lengths: A [batch_size] vector of true sequence lengths.
transition_params: A [num_tags, num_tags] transition matrix.
Returns:
sequence_scores: A [batch_size] vector of unnormalized sequence scores.
"""
# If max_seq_len is 1, we skip the score calculation and simply gather the
# unary potentials of the single tag.
def _single_seq_fn():
batch_size = array_ops.shape(inputs, out_type=tag_indices.dtype)[0]
example_inds = array_ops.reshape(
math_ops.range(batch_size, dtype=tag_indices.dtype), [-1, 1])
sequence_scores = array_ops.gather_nd(
array_ops.squeeze(inputs, [1]),
array_ops.concat([example_inds, tag_indices], axis=1))
sequence_scores = array_ops.where(math_ops.less_equal(sequence_lengths, 0),
array_ops.zeros_like(sequence_scores),
sequence_scores)
return sequence_scores
def _multi_seq_fn():
# Compute the scores of the given tag sequence.
unary_scores = crf_unary_score(tag_indices, sequence_lengths, inputs)
binary_scores = crf_binary_score(tag_indices, sequence_lengths,
transition_params)
sequence_scores = unary_scores + binary_scores
return sequence_scores
return utils.smart_cond(
pred=math_ops.equal(
tensor_shape.dimension_value(
inputs.shape[1]) or array_ops.shape(inputs)[1],
1),
true_fn=_single_seq_fn,
false_fn=_multi_seq_fn)
其中crf_unary_score表示输入观测到标记状态的得分,crf_binary_score表示标记状态间转移的得分。和上述条件随机场的参数化形式中的参数解释部分的得分相对应。
再调用crf_log_norm计算归一化因子的对数数值,两项相减得出最终的对数概率。[相关计算可参考Neural Architectures for Named Entity Recognition中的式(1)]
通过上述损失函数,利用一定的训练数据集,可学习出转移参数transition_params。
在预测阶段利用学习到的转移参数transition_params调用tensorflow中的解码函数crf_decode或viterbi_decode即可得到标注序列。crf_decode与viterbi_decode实现了相同的功能,前者是基于tensor实现的,后者是基于numpy实现的。
重点看下crf_decode的使用,其定义如下
tf.contrib.crf.crf_decode(
potentials,
transition_params,
sequence_length
)
其中potentials表示待预测句子经过双向LSTM的输出,transition_params为训练过程学习到的参数,sequence_length为待预测句子的实际长度
具体实现如下
def crf_decode(potentials, transition_params, sequence_length):
"""Decode the highest scoring sequence of tags in TensorFlow.
This is a function for tensor.
Args:
potentials: A [batch_size, max_seq_len, num_tags] tensor of
unary potentials.
transition_params: A [num_tags, num_tags] matrix of
binary potentials.
sequence_length: A [batch_size] vector of true sequence lengths.
Returns:
decode_tags: A [batch_size, max_seq_len] matrix, with dtype `tf.int32`.
Contains the highest scoring tag indices.
best_score: A [batch_size] vector, containing the score of `decode_tags`.
"""
# If max_seq_len is 1, we skip the algorithm and simply return the argmax tag
# and the max activation.
def _single_seq_fn():
squeezed_potentials = array_ops.squeeze(potentials, [1])
decode_tags = array_ops.expand_dims(
math_ops.argmax(squeezed_potentials, axis=1), 1)
best_score = math_ops.reduce_max(squeezed_potentials, axis=1)
return math_ops.cast(decode_tags, dtype=dtypes.int32), best_score
def _multi_seq_fn():
"""Decoding of highest scoring sequence."""
# For simplicity, in shape comments, denote:
# 'batch_size' by 'B', 'max_seq_len' by 'T' , 'num_tags' by 'O' (output).
num_tags = tensor_shape.dimension_value(potentials.shape[2])
# Computes forward decoding. Get last score and backpointers.
crf_fwd_cell = CrfDecodeForwardRnnCell(transition_params)
initial_state = array_ops.slice(potentials, [0, 0, 0], [-1, 1, -1])
initial_state = array_ops.squeeze(initial_state, axis=[1]) # [B, O]
inputs = array_ops.slice(potentials, [0, 1, 0], [-1, -1, -1]) # [B, T-1, O]
# Sequence length is not allowed to be less than zero.
sequence_length_less_one = math_ops.maximum(
constant_op.constant(0, dtype=sequence_length.dtype),
sequence_length - 1)
backpointers, last_score = rnn.dynamic_rnn( # [B, T - 1, O], [B, O]
crf_fwd_cell,
inputs=inputs,
sequence_length=sequence_length_less_one,
initial_state=initial_state,
time_major=False,
dtype=dtypes.int32)
backpointers = gen_array_ops.reverse_sequence( # [B, T - 1, O]
backpointers, sequence_length_less_one, seq_dim=1)
# Computes backward decoding. Extract tag indices from backpointers.
crf_bwd_cell = CrfDecodeBackwardRnnCell(num_tags)
initial_state = math_ops.cast(math_ops.argmax(last_score, axis=1), # [B]
dtype=dtypes.int32)
initial_state = array_ops.expand_dims(initial_state, axis=-1) # [B, 1]
decode_tags, _ = rnn.dynamic_rnn( # [B, T - 1, 1]
crf_bwd_cell,
inputs=backpointers,
sequence_length=sequence_length_less_one,
initial_state=initial_state,
time_major=False,
dtype=dtypes.int32)
decode_tags = array_ops.squeeze(decode_tags, axis=[2]) # [B, T - 1]
decode_tags = array_ops.concat([initial_state, decode_tags], # [B, T]
axis=1)
decode_tags = gen_array_ops.reverse_sequence( # [B, T]
decode_tags, sequence_length, seq_dim=1)
best_score = math_ops.reduce_max(last_score, axis=1) # [B]
return decode_tags, best_score
return utils.smart_cond(
pred=math_ops.equal(tensor_shape.dimension_value(potentials.shape[1]) or
array_ops.shape(potentials)[1], 1),
true_fn=_single_seq_fn,
false_fn=_multi_seq_fn)
关于命名实体网络结构中CRF部分可参考https://github.com/carlos9310/BERT-BiLSTM-CRF-NER.git中bert_base/train/bert_lstm_ner.py中的add_blstm_crf_layer函数中crf_layer与crf_decode的具体调用(该网络结构在设计时有缺陷,限制了最大文本序列的长度。如果某个实体在长文本的后面,那么在实体识别前会截断过长的部分。利用viterbi_decode进行解码且对文本长度无限制的版本见https://github.com/crownpku/Information-Extraction-Chinese)
def add_blstm_crf_layer(self, crf_only):
"""
blstm-crf网络
:return:
"""
if self.is_training:
# lstm input dropout rate i set 0.9 will get best score
self.embedded_chars = tf.nn.dropout(self.embedded_chars, self.dropout_rate)
if crf_only:
logits = self.project_crf_layer(self.embedded_chars)
else:
# blstm
lstm_output = self.blstm_layer(self.embedded_chars)
# project
logits = self.project_bilstm_layer(lstm_output)
# crf
loss, trans = self.crf_layer(logits)
# CRF decode, pred_ids 是一条最大概率的标注路径
pred_ids, _ = crf.crf_decode(potentials=logits, transition_params=trans, sequence_length=self.lengths)
return (loss, logits, trans, pred_ids)
最后总结下CRF在上述NER中的过程。首先,待标注的句子中的每个词/字,经过向量化后输入到双向LSTM中,得到的输出张量可看成CRF中的状态函数的得分(或HMM中的观测概率矩阵),随机初始化(学习到)的transition_params可看成转移函数的得分(或HMM中的状态转移概率矩阵),由上述确定下的参数,最终预测出概率最高的标注序列。由于CRF考虑到标注序列的前后关系,增加了输出约束,可有效避免不符合逻辑关系的标注序列出现。
补充(crf_decode与viterbi_decode一致性验证)
transition表示训练阶段学习到的转移参数,以NER为例,其表示不同tag间转移的几率。给的代码表示有3种不同的tag。
score表示预测时,根据训练得到的网络结构和参数,计算某个批次中的某句话中的每一个字属于不同tag的几率。给的代码表示一个批次中只有一句话,且该句话有4个字,每个字给出了属于不同tag的几率。
crf_decode与viterbi_decode基于上述两个参数解码出一个最佳的标记序列。其核心思想是基于动态规划与回溯进行解码的。(viterbi = 动态规划+回溯)
具体代码如下,两个解码函数返回同样的结果。
import tensorflow as tf
import numpy as np
from tensorflow.contrib.crf import viterbi_decode
from tensorflow.contrib.crf import crf_decode
score = [[
[1, 2, 3],
[2, 1, 3],
[1, 3, 2],
[3, 2, 1]
]] # (batch_size, time_step, num_tabs)
transition = [
[2, 1, 3],
[1, 3, 2],
[3, 2, 1]
] # (num_tabs, num_tabs)
lengths = [len(score[0])] # (batch_size, time_step)
print(f'lengths:{lengths}')
print(f'shape of np.array(score[0]):{np.array(score[0]).shape}')
print(f'shape of np.array(transition):{np.array(transition).shape}')
# numpy
print("[numpy]")
np_op = viterbi_decode(
score=np.array(score[0]),
transition_params=np.array(transition))
print(np_op[0])
print(np_op[1])
print("=============")
# tensorflow
score_t = tf.constant(score, dtype=tf.int64)
transition_t = tf.constant(transition, dtype=tf.int64)
lengths_t = tf.constant(lengths, dtype=tf.int64)
tf_op = crf_decode(
potentials=score_t,
transition_params=transition_t,
sequence_length=lengths_t)
with tf.Session() as sess:
paths_tf, scores_tf = sess.run(tf_op)
print(f'shape of score_t:{score_t.shape}')
print(f'shape of transition_t:{transition_t.shape}')
print(f'shape of lengths_t:{lengths_t.shape}')
print("[tensorflow]")
print(paths_tf)
print(scores_tf)
其中基于numpy写的viterbi算法比较简洁,具体如下:
def viterbi_decode(score, transition_params):
"""Decode the highest scoring sequence of tags outside of TensorFlow.
This should only be used at test time.
Args:
score: A [seq_len, num_tags] matrix of unary potentials.
transition_params: A [num_tags, num_tags] matrix of binary potentials.
Returns:
viterbi: A [seq_len] list of integers containing the highest scoring tag
indices.
viterbi_score: A float containing the score for the Viterbi sequence.
"""
trellis = np.zeros_like(score)
backpointers = np.zeros_like(score, dtype=np.int32)
trellis[0] = score[0]
for t in range(1, score.shape[0]):
v = np.expand_dims(trellis[t - 1], 1) + transition_params
trellis[t] = score[t] + np.max(v, 0)
backpointers[t] = np.argmax(v, 0)
viterbi = [np.argmax(trellis[-1])]
for bp in reversed(backpointers[1:]):
viterbi.append(bp[viterbi[-1]])
viterbi.reverse()
viterbi_score = np.max(trellis[-1])
return viterbi, viterbi_score
其中trellis保存的是到每一个字标记为不同tag时对应的总分数最大。backpointers记录的是由上一个字到当前字标记为不同tag时对应的总分数最大时上一个字对应的tag的索引,到遍历完所有字时,可确定最后一个字对应的tag索引,然后根据最后一个字的索引,从backpointers中回溯其上一个字对应的tag的索引,直到回溯到第一个字,最终得到每个字对应的tag使总的分数最大。
以上便是viterbi算法的大致流程。